Among the many things RSBs record for me are helicopter passes. Medical, police, and military flights are common here, but there are some others like passenger flights and power line inspections too. They often stand out very well on my RSB, both in the infrasound and in the seismic channels. Somewhat to my surprise, the seismic signal is cleaner than the infrasound. Perhaps there are more reflections in audio and hence more of a thunder-like rumble.
This page looks at a single fast pass of a Sikorsky Black Hawk. Here are all the traces recorded.
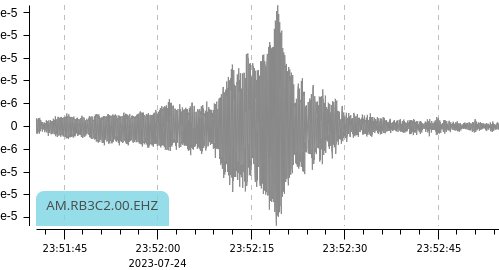
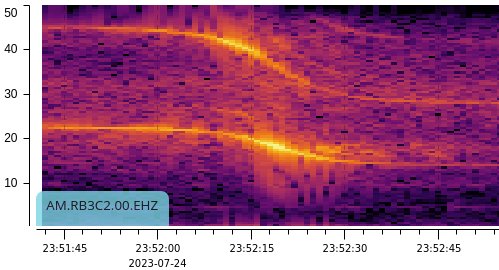
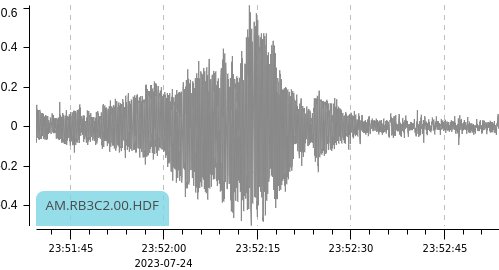
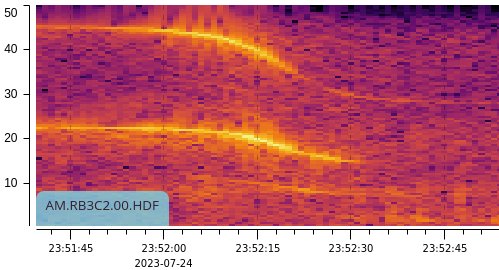
| Amplitude | Spectrum | |
| Seismic |  |
 |
| Infrasound |  |
 |
The envelope of the traces differ. I suspect one thing going on is that the more distant seismic signals take multiple paths from helicopter to ground to RSB and that the acoustic signals mostly reflect off the ground, much as light does reflecting off water. However, that's not germane to this page.
Much more interesting to us are the declining frequecies in the spectrograms. Each has two main signals, a fundamental tone and the first harmonic. The latter is easier to read from the graph than the fundamental, so I focus on that, and the frequency drops from 46 Hz to 27 Hz. Given that, what's the velocity of the helicopter?
Most descriptions of the Doppler effect provide both the velocity of the source (and/or the observer) and the frequency emitted by the source. We want the former, we don't really care about the latter. The geometry of this puzzle lends itself to work with the wavelengths first, and then convert to the frequencies we can read off the graph. It seemed to me that there ought to be a simple, elegant equation to convert those frequencies to the velocity. It turns out that there is.
First, consider these two extreme cases, one with a pulsating sound source that is not moving at all, and then with it moving to the right at Mach 0.9:
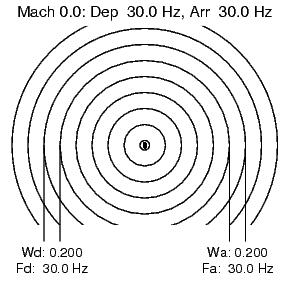
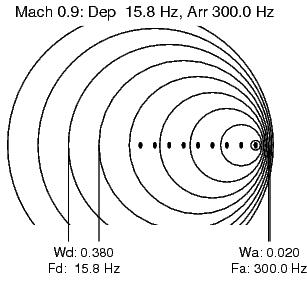
In the motionless case, the wavelength always matches that of the source frequency, of course. In the Mach 0.90 case, the source is moving left to right and that motion adds (and subtracts) to the trailing (and leading) sound pulses. Note that as the source gets closer to Mach 1 the trailing wavelength approaches twice the motionless case and the leading wavelength approaches zero. The wavelengths' units are arbitrary and come from the spacing of my original plots on paper.
Here's the more realistic case of Mach 0.25. There's little to add to the description:
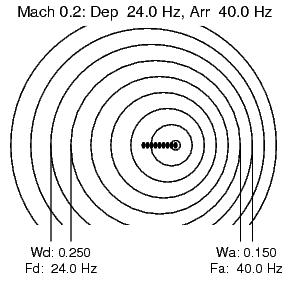
With those visual aids, we can shift to the algebra behind all this. We're dealing with these variables:
The variables use these subscripts to connect them to the objects:
| The wavelengths the observers see depends on the velocity of the source |
\(w_d = w_s \times \frac{c + v}{c}\) \( w_a = w_s \times \frac{c - v}{c} \) |
| Solving for \( w_s \) | \( w_s = {w_d} \times \frac{c}{c + v} = w_a \times \frac{c}{c - v} \) |
| Flipping to start using frequencies | \( f_s = f_d \times \frac{c + v}{c} = f_a \times \frac{c - v}{c} \) |
| Dropping \( f_s \) and that \( c \) | \( f_d(c + v) = f_a(c - v) \) |
| Expanding the multiplication | \( f_d{c} + f_d{v} = f_a{c} - f_a{v} \) |
| Get just the \( v \) terms on the left | \( f_a{v} + f_d{v} = f_a{c} - f_d{c} \) |
| Factoring | \( v(f_a + f_d) = c(f_a - f_d) \) |
| Solving for \( v \) yields Ric's equation | \(v = c \times \frac{f_a - f_d}{f_a + f_d}\) |
| In miles per hour | \(v = 760 \times \frac{f_a - f_d}{f_a + f_d}\) |
| In kilometers per hour | \(v = 1225 \times \frac{f_a - f_d}{f_a + f_d}\) |
Note that at small doppler shifts \( f_a - f_d \) will be small and the equation will yield a low speed. At large shifts, \( f_a \) dominates the equation and speed will be close to the speed of sound. Simple and elegant, as I hoped.
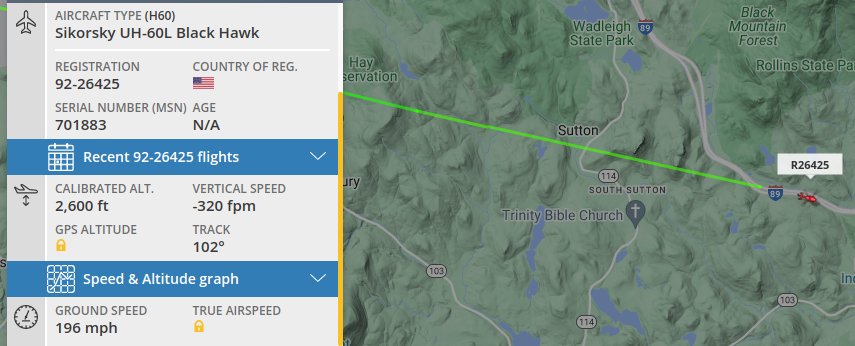
Back above I noted that the frequency drops from 46 Hz to 27 Hz. Therefore, the speed is \( 760 \times \frac{46 - 27}{46 + 27} = 198 \) mph. While those frequencies are imprecise, they fit better than I expected. This image from FlightRadar64.com reports 196 mph:
While I did pick this trace for the big difference in frequencies, there's a bit of a catch. Wikipedia's Sikorsky UH-60 Black Hawk web page states:
I don't have the air speed, I'll just assume it had a tail wind. I believe my equation is computing the ground speed - if the air speed equals a headwind's speed, then the helicopter will be motionless and you'll hear the source frequency.
Yes, calling this Ric's Equation is more than a bit presumptuous. However, after I derived this, I went looking for it on the web - and didn't find it! Pretty much everything I found started with the source velocity and frequency, then derived the frequency the observers would hear. I conclude that before Raspberry Shakes showed up few people were interested in what our RSBs hear.
Written 2025 Mar 24, last updated 2025 Jul 28.