
A long, long time ago when I heard about the Flat Earth Society I assumed it was a British Social club conceived in British humor, something I've never quite understood. I was shocked when I discovered that the twits were serious, something I will never understand.
Various events over a decades made me realize that we can see that Earth is round from a jetliner. These include:
There's a concise formula that gives a good estimate of the distance to the horizon in
miles given your altitude in feet.
It's just distance = 1.22 × sqrt(height)
The math behind it is surprisingly simple and is merely based on the Pythagorean Theorem
That math also yields the "dip angle" between the horizon and the horizontal.
It's surprisingly large, over 3° at typical flight levels.
The lower atmosphere has a variable index of refraction with height, however it's no
more than 0.5° from off the Earth to the horizon. It makes the horizon farther away and
reduces the dip angle.
This occurred to me during a flight, and using the spine of the in-flight magazine as a straight edge I could hold it to make it appear tangent to the Earth's surface and could readily see the Earth's surface was curved.
Recently I flew to the Pacific Northwest and decided to bring a better straightedge, i.e. a drafting ruler with a triangular cross section, tape it across the window, and photograph the scene. Then it occurred to me that my cellphone camera has two leveling lines, one shows the center of the field of view, the other shows the camera's tilt and pitch. When they overlay each other the camera is level on both axes. That means I could make screen captures without attaching the ruler to the window and making other measurements in flight to calculate the dip. Even better, I could do it without attracting the attention of the flight attendants.
The following photographs were taken with a Pixel-7 cell phone at a Zoom value of 2. This is not a "computed zoom," it's the inner 1/4 pixels of the imager, and a setting that's easy to choose. I need to determine the field of view at this zoom value. That will let me easily measure the dip angle. Not tonight.
This first image is from the Puget Sound in Washington State. It is merely confirmation that when the camera's guidelines overlay when the camera is aimed horizontally and that the reference lines are on the horizontal plane and in the center of the image. The 1° refers to the camera being tilted 1°. To make the screen captures I had to press two control buttons simultaneously through the Otter Box protective shell. It's hard to do that while keeping the camera oriented well.

This image is a daytime shot from the air with cloud on the horizon. Here the horizon is clearly below the horizontal plane.

These late twilight shots have the ground as the horizon, Bismark, North Dakota is in the foreground. At this point in the trip, the plane's altitude was 34,300 feet, Bismark is at 1,700 feet, and about 50 miles away in the latter photo. The horizon should be some 220 miles away, close to the Canadian border and the dip angle about 3.2°. I'm surprised there was still twilight to be seen - for future play, that point is about 49.0N 102.7W, date May 8th, time 2321 EDT. I remember camping one night 50 years ago in early July on the Montana border and couldn't make out all the stars in the Big Dipper until 2230 MDT or something like that.
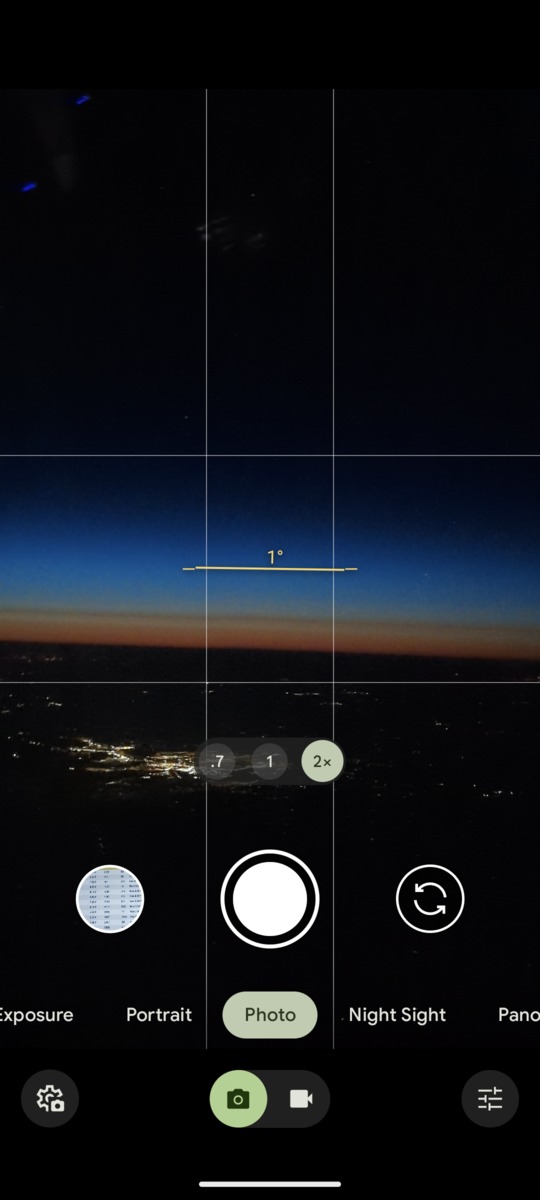
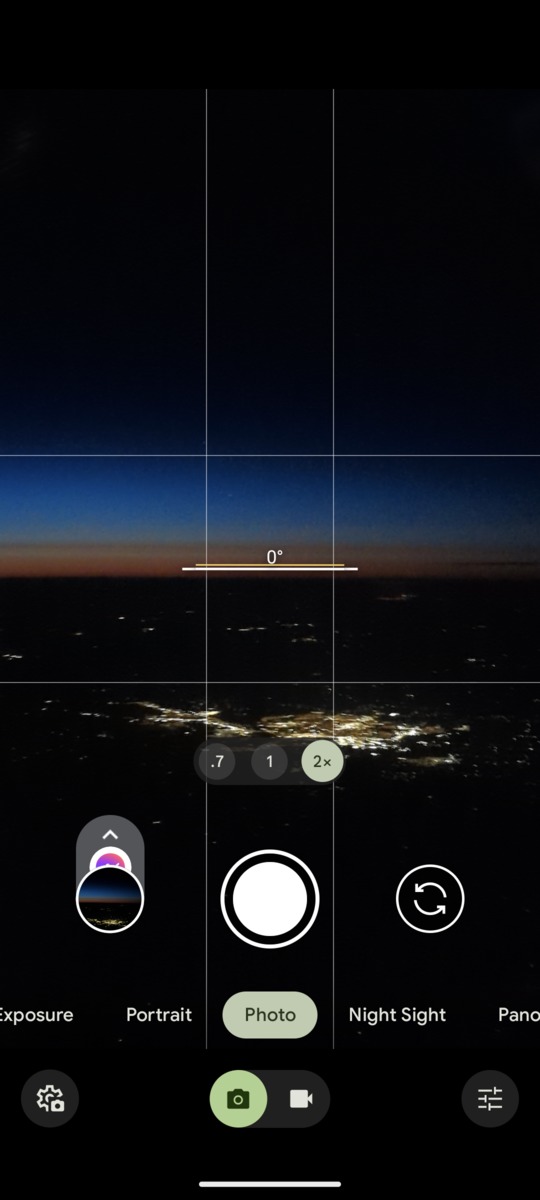
It's clear to me that this is strong evidence for a curved Earth. It's just as clear to me that flat Earthers will try to blame things on a prismatic cross section in airplane windows or other overstated second order effects. I won't waste my time trying to convince them otherwise, I'm just happy to have my own page to share with them.
While poking around a bit, I didn't come across many photos from airplanes documenting the curvature of the Earth. I suspect that a lot of fellow geeks don't realize that the horizon dip angle is so easy to compute, let alone capture from 30,000+ feet. I hope to see more photos from you guys in the future.
I'm somewhere between disappointed and appalled at the references I'm finding. It look's like I'll have to make some of my own drawings and do the math myself. Guys, it's not that hard....
https://en.wikibooks.org/wiki/Trigonometry/The_distance_and_dip_of_the_horizon
Decent description, no image. Oops, I take that back - it has a blatant math error that was
added over ten years ago!
https://www.siranah.de/html/sail040o.htm
Decent images that include atmospheric refraction, but the math is more trig than geometry
and uses some odd notation.
https://aty.sdsu.edu/explain/atmos_refr/dip.html
This is probably the best I've seen. It's focus is on refraction, but it describes the
non-refractive case well first.
Written 2024 May 26, last updated 2024 May 27.