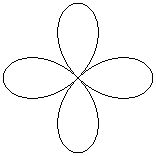
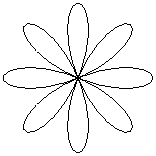
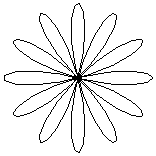
| Even Orders | |||
|---|---|---|---|
| 0 | 2 | 4 | 6 |
 |
 |
 |
 |
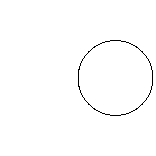
| Odd Orders | |||
|---|---|---|---|
| 1 | 3 | 5 | 7 |
 |
 |
 |
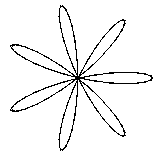 |
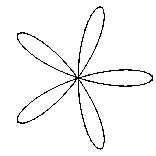
A long time ago, I was an undergrad at Carnegie-Mellon University and a parttime computer operator for their PDP-10 computer. The Computer Science Department had several people from Stanford, and occasionally, a "Care" package would arrive to keep the ex-pats up to date. One odd little Sail program was called "Petal," I believe, and it drew interesting and attractive patterns on an early display terminal called the ARDS. It was soon apparent that the author had written a program to display a plane curve called a Rose. It's a simple, but attractive, curve with polar equation r = a × cos(nθ). For our purposes, a is 1 and can be ignored, n is the "order" of the rose and affects the number of lobes on the curve. Various roses look like:
| Even Orders | |||
|---|---|---|---|
| 0 | 2 | 4 | 6 |
 |
 |
 |
 |
| Odd Orders | |||
|---|---|---|---|
| 1 | 3 | 5 | 7 |
 |
 |
 |
 |
Furthermore, the author had forgotten that Sail's trig functions expected radians, and the program supplied degrees. The erroneous result was more interesting than the expected result and the author made some tweaks to explore patterns, most which had never before been seen.
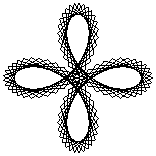
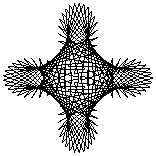
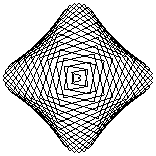
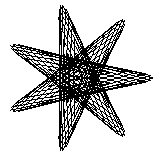
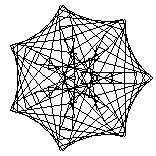
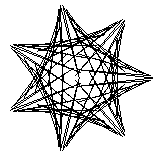
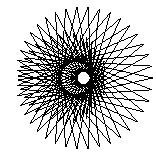
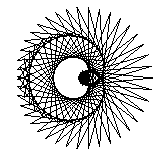
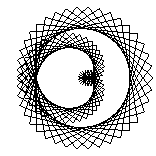
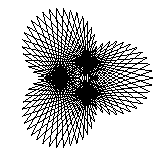
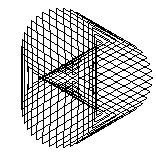
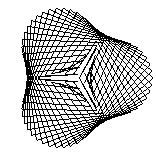
The two key parameters we could change were the "Style", basically the delta-theta between points, and order, which we called "Petal". While not exactly matching the Stanford program, when either of these are too big to draw the curve accurately, interesting patterns appear, as in these patterns drawn with 99 vectors:
| Style | |||||
|---|---|---|---|---|---|
| 1 (3.6°) | 8 (29.1°) | 16 (58.2°) | 25 (90.9°) | ||
| P e t a l |
2 |  |
 |
 |
 |
| 7 |  |
 |
 |
 |
|
| 20 | 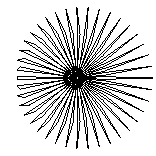 |
 |
 |
 |
|
| 32 |  |
 |
 |
 |
|
A few years later I was looking for a project to learn more about PDP-11 assembly language programming and was torn between an early laser printer and a vector graphics system that was finally becoming usable. The grad students used the laser printer to print their theses, and while I was walking to the Coke machine, one asked for help. I saw the light and foresaw the whole department pestering me with theses that had to be done tonight. A few minutes later I realized the new graphics system might display petal effects we hadn't seen on the ARDS.
Ultimately I discarded the degrees vs. radians math for a simpler design where I made the delta-theta step size a multiple 1/2880 of a circle (1/8 degree). This allowed the patterns to close, i.e. the start and end points were the same r = 0, θ = 0° and selecting the step size allowed patterns with few or many vectors. All in all, this was a great improvement.
The vector graphics hardware indeed disclosed shapes we hadn't seen before and haven't seen since. Instead of the electron beam scanning the screen as in raster graphics, the beam traces each line in the image. Where the lines cross, the crossing point gets brighter, in raster graphics they usually don't. The result was that complex patterns had a lacy effect, and features that had curves due to multiple vectors laid close together had a fluted 3D effect. On the ARDS storage tube and the raster displays in the next generation such areas wash out the details and loose much of the 3D appearance.
At any rate, one of the hardware designers got permission to enter the system in the Three Rivers Art Festival and it was accepted. He built a separate keypad for visitors to use and I added support for it. It was one of the hits of the show and made it on to the evening TV news.
In 1974 I left CMU for DEC (Digital Equipment Corp) and talked about my nifty hack with some of my new coworkers. I soon wrote a version in Fortran for the VT11, DEC's vector graphics system that was really no match for CMU's Graphic Wonder. I called that one Petal, so when I had time to port my assembly language version I decided to call the new one Roses.
That wound up being used as an attention getter at some computer shows and was displayed in a computer art show at the Worcester Art Museum.
Since then I've written Roses programs in various languages and graphics libraries to learn about them. The algorithm is so simple it only takes a few lines of code, and that lets me concentrate the language or user interface. I've even used a spreadsheet to display patterns (all you need is something that display X-Y graphs).
Several years ago I chose (correctly!) to learn and use Python for most programming projects, and after "Hello, World," "Recursive Fibonacci," and "Primes," I embarked on Roses with the tkintr interface. I learned what I needed, and never dealt with window resizing or other hassles. Soon after that, wxPython appeared and was getting much positive attention, so I added that to the list of things to do "someday". That day finally arrived in 2007 and I found that the positive comments were not for "ease of use" but for the completeness of the wxPython/wxWidgets package. However, that day (weeks, actually) I had time to polish a number of features ignored since the PDP-11 version.
The result is the first version worth sharing with people since my PDP-11 days, and Robin Dunn has helped tweak it further. It has been accepted into the wxPython/samples directory of the wxWidgets distribution, but I'll keep source outside of github here. These Web pages are not in the distribution.
wxroses.html describes what little wxPython knowledge I know, i.e., all I needed to use it with roses.
The software is in two files:
Download both files to a system that has Python and wxPython installed. Note: the files all have a ".py.txt" extension at the server, you'll need to rename the files to drop the ".txt" part. Running python wxroses.py and clicking on the "Use GCDC" check box should show:
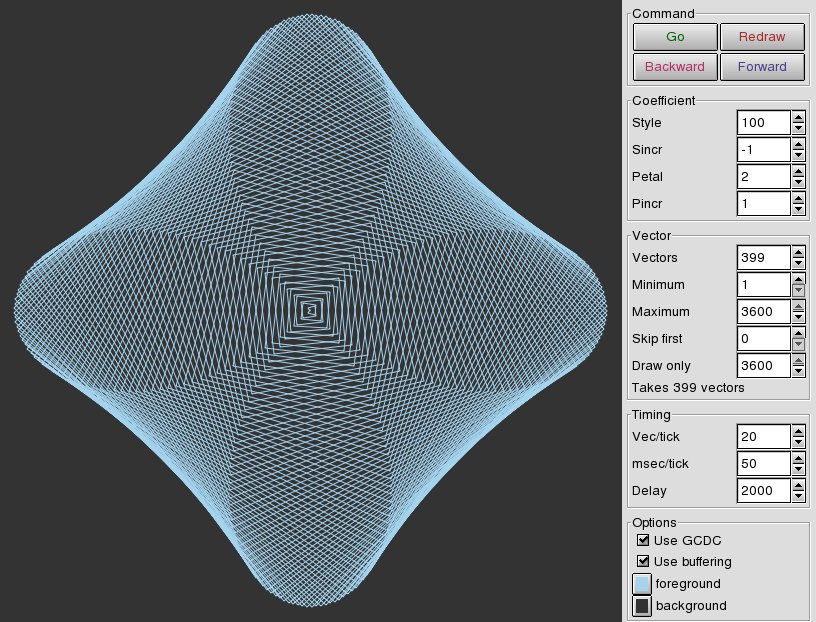
While the analytic geometry definition of a rose, r = a × cos(nθ) has only one substantive parameter, "n," drawing the curve on a digital computer needs one more, and misdrawing it into something interesting implies a third.
Mathematically the "n" above is called the "order" of the rose. The rose curve has a number of lobes, or petals, a friendlier name. When the order is even, it has twice that number of petals. When the order is odd, it has just that number of petals. The reason is that even order roses need θ to go over the entire range [0 .. 2π] range. In odd order roses when θ = π (180°), r is -1 and the curve is at the starting point already.
A stuffier name might be granularity. A digital computer displaying a rose has to use a finite number of points along the curve and "connect the dots," generally with straight lines, i.e. vectors. 50 vectors or so will do a very good job drawing a circle on most displays. 50 times the rose's order will do pretty well for real roses.
However, you'll soon tire of accurately drawn roses because misdrawing them yields more interesting effects. Most of the time you will be exploring patterns with more lobes than the number of vectors can draw "well."
Instead of going point-to-point around the rose, we can go every "x" steps. If we sample 360 points but use every other, we get back to the starting point with 180 vectors. All we've done is the equivalent of requesting fewer vectors. If we sample every seventh point, we'll pass the starting point in 360/7 or 51+ points. Only when we make the seventh circuit will we reach the start again. I call this sampling rate the Style because you get similar effects if you change the order by two.
If you sampled every 90 degrees of an even ordered rose, you'll draw a square. Boring. If you sampled slightly further than 90 degrees, then after four vectors you'll have almost a square but are a little bit too far along the curve. Four vectors later and you'll draw a slightly smaller square that's rotated a bit. As it continues, new squares get smaller and rotate down into the center and then climb back out. It's fun to watch and the overlapping squares make fascinating moire patterns.
These are the three key parameters, you'll find them in the control boxes on the left side of the screen. In general, set the number of vectors based on the maximum complexity you want to see, then set the order low if you want lobes around the outside or higher if you want to see "aliasing" effects. Then experiment with different styles.
Petal and Vectors determine the vertexes of the pattern, Style determines how they are connected. If Style and Vectors have common factors, the pattern won't connect all the vertexes. For example, if you set Style to 99, that shares a factor of 3 with Vectors, and connecting every third vertex gets use back to the beginning with only 133 vectors. For Style 98, 7 is a common factor, and only 57 vectors will draw the pattern. 97 is prime, so that style will need all vertexes.
In automatic mode, the labels on the buttons and the functions change:
The Minimum and Maximum parameters in the Vector control panel can filter the patterns wxRoses will display while in automatic mode. Only patterns that have at least Minimum vectors and no more than Maximum will display. It can be quite jarring to be watching complex patterns go by and suddenly see a triangle. That was more of an issue on the PDP-11 versions where the number of vectors was fixed at 2880 (CMU) or 2520 (DEC). If you set Vectors to a prime number, then you will always need that many vectors for a pattern.
The "Skip first" and "Draw only" parameters are most useful for some simple animations. In general you'll want "Skip first" to be 0-5, "Draw only" to be 10-15, Pincr 0, Sincr 1, and Delay 10-50. In automatic mode you should see a simple shape transform as Style increases.
In automatic mode, wxRoses waits "Delay" msec between patterns. Increase it to "savor" a pattern longer, decrease it if you're the impatient sort. Or click Skip if you're the impatient domineering sort.
The "Use buffering" checkbox defaults to on. Exposure events, dragging other windows over wxRoses, etc. will all restore the window without redrawing the pattern. When this is disabled, then any exposure event schedules redrawing the pattern from scratch.
"Foreground" and "Background" will bring up a rather nice colour dialog that serves mainly to remind us that we ought to be doing something interesting with color changes while drawing.
A online computer history features early graphics systems and people. It has pictures of an ARDS, a PDP-11/45, a Tektronix 4010 (and ARDS-like display that sold well), a small CalComp plotter, and Doug Englebart's first mouse. Discounting the 4010 and mouse, that's three historical items directly connected to Roses. It also has pictures and text of other key items like the PDP-1, Spacewar, the Rand tablet, that are not directly connected to Roses. And a mention of the PDP-10.
The CMU folks who developed the Graphic Wonder went on to create Three Rivers Computer Corp and the PERQ, the first commercially available workstation. Yes - the roses images are inspired by my program.
Euclidean Geometry is taught in high school, that's the geometry that focuses on proofs derived from previous proofs, straightedges, and compasses. Schools largely ignore Analytic Geometry, which focuses on curves produced from equations applied in various reference frames. Schools generally get no deeper than conics (ellipses, parabolas, and hyperbolas) and often don't bother to use the term "Analytic Geometry."
That's kind of a shame, because some of the curves have interesting properties that couple into everyday life. E.g. a catenary curve is the shape a hanging rope makes, cardioids show up in microphone and antenna reception patterns, and cycloids could make a perfect pendulum or "ideal" low energy transportation tunnels (and completely impractical, but interesting nonetheless). I'm not sure what piqued my interest in analytic geometry, but I still have a plot I made during high school polar plots of trig functions, including r = cos(θ). In college I bought the Dover book Catalog of Special Plane Curves. On the web, by far the best source is Eric Weisstein's extensive collection, see his page on the rose and explore from there.
These days, computers make exploring these curves easy and various math packages make them trivial. This makes me especially disappointed that Analytic Geometry seems less popular than it was before the tedium was removed. (Fractals, on the other hand, exploded in large part due to inexpensive computational resources required for many images.) Even 3D surfaces are easy to render, which means I ought to return to some of the 3D roses I experimented with briefly back at CMU. Don't expect that anytime soon.
Contact Ric Werme or return to his home page.
Last updated 2017 February 11 to update links, first written 2007 June 13.