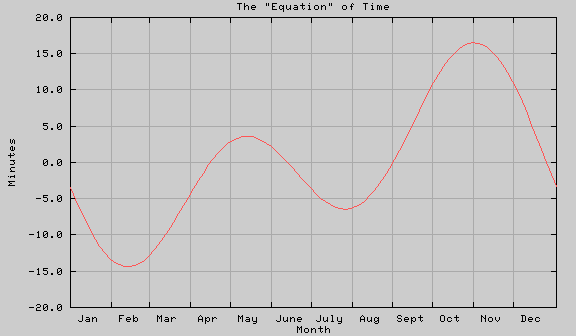
In the northern temperate zone, the earliest sunset of the year occurs a couple weeks before the winter solstice, and the latest sunrise occurs a couple weeks after the solstice. (Stranger things happen at the poles and near the equator.) The reason for this involves the Equation of Time.
Noon used to be when the Sun crossed the meridian, the line going from the North horizon, through the zenith (the point overhead) and down to the south horizon. The difficulties this caused with train schedules led to the invention of standard time and the Earth's time zones. I don't know who came up with daylight time, but double daylight was installed during WWII as an energy conservation measure. Along with the transition from telling time with sundials to telling time with clocks, people realized that the time from one noon to the next was not constant. Part of the jargon invented to deal with the situation is "sun time", the time a sundial would tell, and "mean time", the time an accurate clock would tell. The difference between the two is an error that has come to be called the "Equation of Time". It is usually described as a table, plotted as the error vs. the Sun's declination, or plotted a graph of error vs. date:

For this graph, I used the equation:
Please note this is a crude approximation and leaves out lots of detail. In particular, the E1 and E2 components are not really sinusoids. They are periodic, so they can be described by fourier transforms. All I've done is used the first term, which is accurate to a few seconds. Just don't try to reverse engineer the theory from my equation!
The E1 component is due to the eccentricity of the Earth's orbit. The d-2 term reflects the perihelion early in January. When the Earth is near perihelion, its angular velocity with respect to the Sun is higher than average and the Sun's motion in the sky lags a bit.
The E2 component is due to the tilt of the Earth's axis. The d-80 term reflects the vernal equinox about 80 days into the year (31 in Jan., ~28 in Feb., ~21 in March). Pretend the Earth doesn't rotate and its orbit is circular. The Sun is directly above the equator at the vernal equinox. Each day this subsolar point shifts by 1/365 of a track around the Earth, just about one arc degree. This track is tilted from the equator by Earth's tilt of 23.44 degrees, so the longitude change per day is cos(23.44) of that 1/365. When the Sun crosses the Tropic of Cancer, then it would be moving at right angles to longitude lines, but they'd be closer together and the sun would make up the lost time. The effect is exactly analogous to the problem a universal joint has going through a large angle.
An interesting thing about this component is what happens with increasing tilt. The real equation involves transforming the motion of the Sun in the ecliptic (which would be constant were the Earth's orbit a circle) into the apparent motion relative the equator. This transformation is:
cos(23.44) = 0.917, so Q and C don't differ by much. However, the cosine falls off rapidly with greater angles, and a greater tilt would result in a highly disproportionate increase in its effect.
Is any of this worth remembering? Beats me. I got interested for reasons too complex to go into here. The points I like are:
Further references:
I wrote this in the mid 1980's as a USENET sci.astro posting for the perennial question about the earliest sunset/latest sunrise. At least one amateur astronomer saved this in a WWW page and two professional astronomers have given it out the media. Feel free to do the same.
Most recently, I submitted it as an answer to the Mount Washington Observatory's Weather Notebook.
For lots more (including animations) on analemmas and the astrophysics behind them, visit www.analemma.com.
Finally, the perceptive folks at Web Geek Science liked this page enough to translate it into Haitian Creole. I never would have guessed that would be the first target language, but I'm happy to share the content!
Contact Ric Werme or return to his home page.
Last updated 2012 February 2.